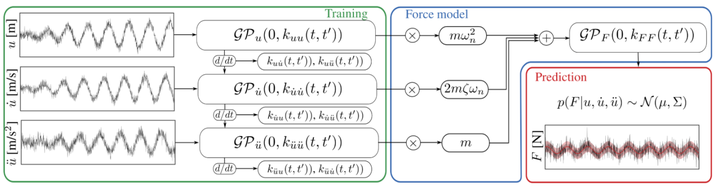
Abstract
Long-span bridges are subjected to a multitude of dynamic excitations during their life span. To account for their effects on the structural system, several load models are used during design to simulate the conditions that the structure is likely to experience. These models are based on different simplifying assumptions, and are generally guided by parameters that are stochastically identified from measurement data, making their outputs inherently uncertain. This paper presents a probabilistic physics-informed machine learning framework based on Gaussian process regression for reconstructing dynamic forces based on measured deflections, velocities, or accelerations. The model can work with incomplete and contaminated data and offers a natural regularization approach to account for noise in the measurement system. An application of the developed framework is given by an aerodynamic analysis of the Great Belt East Bridge. The aerodynamic response is calculated numerically based on the quasi-steady model, and the underlying forces are reconstructed using sparse and noisy measurements. Results indicate a good agreement between the applied and the predicted dynamic load, and can be extended to calculate global responses and the resulting internal forces. Particular uses of the developed framework include validation of design models and assumptions, as well as prognosis of responses to assist in damage detection and structural health monitoring.