Stochastic stiffness identification and response estimation of Timoshenko beams via physics-informed Gaussian processes

Abstract

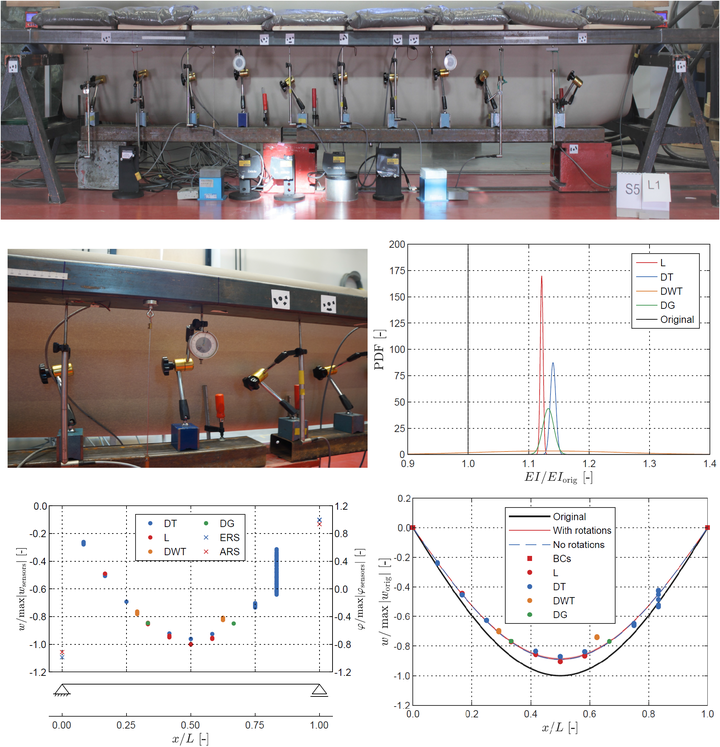
Machine learning models trained with structural health monitoring data have become a powerful tool for system identification. This paper presents a physics-informed Gaussian process (GP) model for Timoshenko beam elements. The model is constructed as a multi-output GP with covariance and cross-covariance kernels analytically derived based on the differential equations for deflections, rotations, strains, bending moments, shear forces and applied loads. Stiffness identification is performed in a Bayesian format by maximising a posterior model through a Markov chain Monte Carlo method, yielding a stochastic model for the structural parameters. The optimised GP model is further employed for probabilistic predictions of unobserved responses. Additionally, an entropy-based method for physics-informed sensor placement optimisation is presented, exploiting heterogeneous sensor position information and structural boundary conditions built into the GP model. Results demonstrate that the proposed approach is effective at identifying structural parameters and is capable of fusing data from heterogeneous and multi-fidelity sensors. Probabilistic predictions of structural responses and internal forces are in closer agreement with measured data. We validate our model with an experimental setup and discuss the quality and uncertainty of the obtained results. The proposed approach has potential applications in the field of structural health monitoring (SHM) for both mechanical and structural systems.