Abstract
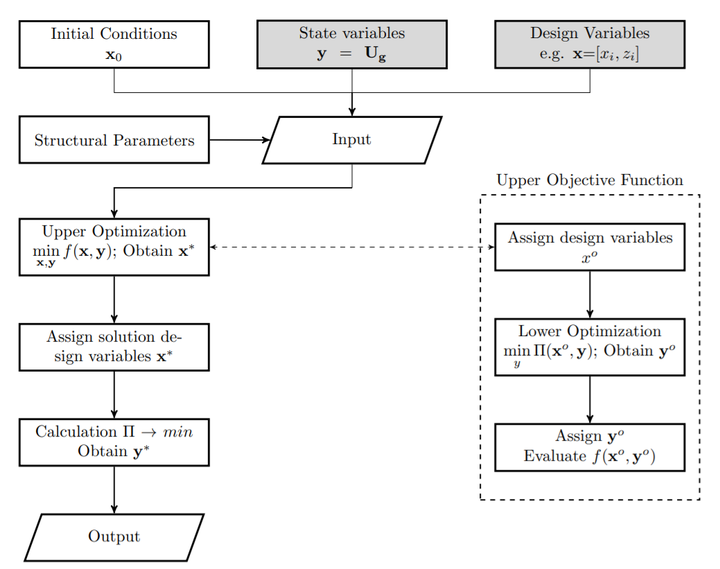
Structural optimization has gained considerable attention in the design of structural engineering structures, especially in the preliminary phase. This study introduces an unconventional approach for structural optimization by utilizing the Energy method with Integral Material Behavior (EIM), based on the Lagrange’s principle of minimum potential energy. An automated two-level optimization search process is proposed, which integrates the EIM, as an alternative method for nonlinear structural analysis, and the bilevel optimization. The proposed procedure secures the equilibrium through minimizing the potential energy on one level, and on a higher level, a design objective function. For this, the most robust strategy of bilevel optimization, the nested method is used. The function of the potential energy is investigated along with its instabilities for physical nonlinear analysis through principle examples, by which the advantages and limitations using this method are reviewed. Furthermore, optimization algorithms are discussed. A numerical fully functional code is developed for nonlinear cross section, element and 2D frame analysis, utilizing different finite elements and is verified against existing EIM programs. As a proof of concept, the method is applied on selected examples using this code on cross section and element level. For the former one a comparison is made with standard procedure, by employing the equilibrium equations within the constrains. The validation of the element level was proven by a theoretical solution of an arch bridge and finally, a truss bridge is optimized. Most of the principle examples are chosen to be adequate for the everyday engineering practice, to demonstrate the effectiveness of the proposed method. This study implies that with further development, this method could become just as competitive as the conventional structural optimization techniques using the Finite Element Method.